티스토리 뷰
[1] 상관분석
1) 상관계수
- 범위 : -1 ~ 1
-두 변수의 연관성을 파악하기 위해 사용함.
ex) 주가와 금 가격의 관계 등
-우상향 또는 우하향하는 단조적 관계를 표현함 ↓

-복잡한 비단조적 관계는 잘 나타내지 못함 ↓

| < 상관계수 해석하기 > | ||
| 부호 | + | 두 변수가 같은 방향으로 변화 (하나가 증가하면 다른 하나도 증가) |
| - | 두 변수가 반대 방향으로 변화 (하나가 증가하면 다른 하나는 감소) |
|
| 크기 | 0 | 두 변수가 독립. 한 변수의 변화로 다른 변수의 변화를 예측하지 못함 |
| 1 | 한 변수의 변화와 다른 변수의 변화가 정확히 일치 | |
* 상관계수가 낮다고 해서 관계가 없는 것은 아님 !!
2) 기울기
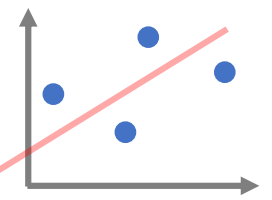
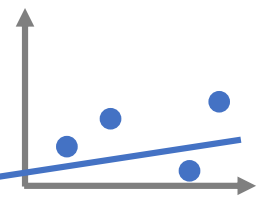
| < 기울기와 상관계수 비교하기 > | ||
| 기울기 | 빨리 올라갈 경우 | 늦게 올라갈 경우 |
 |
 |
|
| 상관계수 | 상관계수 높음 (기울기 상관x) | 상관계수 낮음 |
  |
  |
|
* 기울기는 상관계수와 다른 개념임
3) 공분산
- X의 편차와 Y의 편차를 곱한 것의 평균
(X=Y이면 분산과 같음)

| 우상향하는 추세인 경우 + 로 커짐 | 우하향하는 추세인 경우 - 로 커짐 |
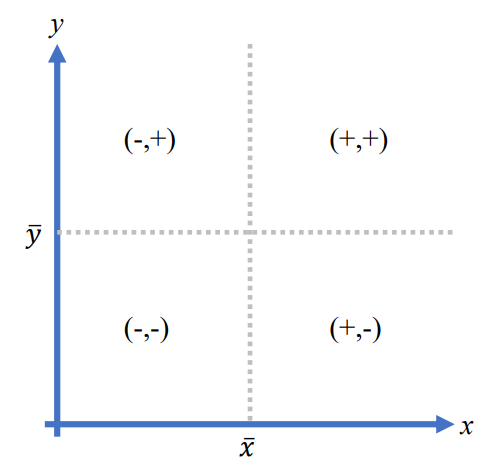
4) 피어슨 적률 상관계수
-범위 : -1 ~ 1
-공분산을 두 변수의 표준편차로 나눔.
-가장 대표적인 상관계수
-선형적인 상관계수를 측정.

5) 스피어만 상관계수 (= 순위 상관계수)
| pg.corr ( X, Y, method='spearman' ) |
- 실제 변수값 대신 그 서열을 사용하여 피어슨 상관계수를 계산.
-표현 : 한 변수의 서열이 높아지면 다른 변수의 서열도 높아지는지?
-두 변수의 관계가 비선형적이나 단조적일 때 사용
ex) 행복과 소득의 상관관계 표현(곡선 상승)
6) 켄달 상관계수
| pg.corr ( X, Y, method='kendall' ) |
-모든 사례를 짝지어 X의 대소관계와 Y의 대소관계가 일치하는지 확인
ex) 소득이 증가하면 행복지수도 올라가는가? (소득 1, 5, 10, 20인 사람 각각 짝지어 비교)

=> 짝의 관계가 True면 1, False면 -1
=> 모든 관계의 점수 합 / 모든 관계의 수 = 상관계수
-모든 데이터끼리 짝을 지어야하기 때문에 데이터가 적을 때 사용.
※ 상관과 인과
| 상관관계 | data.corr( ) |
: 상관관계가 있다고 반드시 인과관계가 있는 것은 아님 !!!
- 제3 변인의 존재
ex) 범죄발생건수 & 종교시설 수의 상관관계 有, 그러나 사실 인구가 많아지면 다 증가함.
- 이질적인 집단들의 합 (심슨의 역설)
- 극단치(outliers)
극단치 有 => 존재하지 않는 상관관계가 나타남, 존재하는 상관관계가 포착되지 못함
'TIL & WIL > 통계분석' 카테고리의 다른 글
| 통계분석 4일차 (4). 다중회귀분석 (0) | 2023.02.16 |
|---|---|
| 통계분석 4일차 (3). 회귀분석 (잔차 / 최소제곱법 / R제곱) (0) | 2023.02.16 |
| 통계분석 4일차 (1). 가설검정 (1) | 2023.02.16 |
| 통계분석 3일차. 독립표본 t 검정/ 효과크기/ 대응표본 t 검정/ 분산분석 (0) | 2023.02.16 |
| 통계분석 2일차. 표집/ 추정/ 통계적 가설 검정/ AB테스팅/ 독립표본 t-검정 (0) | 2023.02.14 |
