티스토리 뷰
▼ 중요해요 ! ▼
[2] 모집단과 표본
-모집단 : 연구의 관심이 되는 집단 전체
-표본 : 특정 연구에서 선택된 모집단의 부분집합
-표집: 모집단에서 표본을 추출하는 절차. "표본추출"이라고도 함.
-대부분의 경우 집단 전체를 전수조사하기는 어려우므로 무작위로 표본을 추출하여 모집단에 대해 추론.
-파라미터 : 어떤 시스템의 특성을 나타내는 값
-모수 : 모집단의 파라미터 : 모집단의 특성을 나타내는 값.
- 통계량 : 표본에서 얻어진 수로 계산한 값 =통계치
※ '모집단의 통계량'이라는 표현은 없음. (=> 모집단의 모수)
※ '표본의 모수' 같은 말도 없음. (=> 표본의 통계량)
-추론통계: 표본 통계량을 일반화하여 모집단에 대해 추론하는 것
-표본이 커지면 커질수록 통계량은 모수 근처에서 나오게 됨
-데이터를 많이 모으면 통계량이 정확하다 = 오차가 적다
1) 표집
: 모집단에서 표본을 추출하는 절차. "표본추출"이라고도 함.
ⓐ 무작위 표집 : 일정한 확률에 따라 표본을 선택 (== 무선표집/ 확률표집)
ⓑ 단순 무작위 표집 : 모든 사례를 동일 확률로 추출 (계통표집/ 층화표집/ 집락표집)
| ⓑ 단순 무작위 표집 | ||
| 계통표집 | - 첫 번째 요소는 무작위로 선정한 후 목록의 매번 n번째 요소를 표본으로 선정 -요소들의 목록이 추출되기 전에 무작위로 되어 있다면 단순 무작위 표집과 거의 동일하면서 조금 더 간단함 -주기성이 있다면 왜곡 가능성이 있음. |
ex) 선거 출구조사 |
| 층화표집 | -모집단을 이루는 각 계층별로 무작위 추출 -모집단이 서로 다른 하위 집단들로 이루어져 있을 경우 |
ex) 지역별/ 연령별/ 성별 여론조사 |
| 집락표집 | -모집단을 집락으로 나눈 후, 집락 중 일부를 무작위로 선택 -선택된 집락에서 표본을 추출 -층화추출과 달리 집락들이 서로 비슷해야 함. |
ex) 같은 도시 학교 중 일부 학교(무작위)의 학생들을 조사 |
2) 표집분포
: 통계량의 분포
- 표준오차: 표집분포의 표준편차
- 모집단이 같아도, 통계량은 표본에 따라 달라짐.
※ 표본의 분포와 표집분포 차이 알기 (예시)
ⓐ 표본의 분포 : 주사위의 숫자가 몇 개 나오는지 각각의 분포
ⓑ 표집분포: 10개의 주사위에서 얻어진 평균점수의 분포
※ 데이터를 많이 모아야 하는 이유?
- 데이터가 많을수록 표준 오차가 작아짐
- 표본의 통계량이 모수에 더 가깝게 나옴
- 표준 오차는 1/√n 으로 줄어들기 때문에, 데이터를 4배 늘리면 2배 더 정확해짐
[3] 추정
: 통계량으로부터 모수를 추측하는 절차
ⓐ 점 추정: 하나의 수치로 추정
ⓑ 구간 추정: 구간으로 추정
1) 신뢰구간
-대표적인 구간 추정방법
-모수가 있을 법한 범위로 추정
-신뢰구간 = 통계량 ± 오차범위
-95% 신뢰구간 = 95%의 경우에 모수가 추정된 신뢰구간에 포함됨.
ⓐ 신뢰구간에 모수가 존재하는 표본의 비율
- 신뢰수준 높음 => 많은 표본(경우) 포함 => 더 넓은 오차범위(&신뢰구간) => 정보가 적음
- 신뢰수준 낮음 => 적은 표본(경우) 포함 => 더 좁은 오차범위(&신뢰구간)=> 정보가 많음
* 신뢰수준 : 얼마나 많은 경우를 포함할까
ex) 96% 신뢰수준 = 96%포함, 4% 배제
ⓑ 신뢰구간이 좁으면 신뢰수준이 낮으므로 타협이 필요
- 교과서적으로는 95%, 99% 등의 신뢰수준을 추천하나, 절대적 기준은 없음
- 감수할 수 있는 수준에서 결정
※ 평균의 신뢰구간
-모든 통계량에는 신뢰구간이 존재
-평균의 경우에는 이론적으로 신뢰구간을 간단히 구할 수 있음
-다른 통계량은 부트스트래핑 등의 복잡한 계산이 필요
2) 부트스트래핑
-평균과 달리 중간값, 최빈값 등의 통계량은 표집분포의 형태를 간단히 알기 어려움
-표본이 충분히 크면 부트스트래핑이라는 시뮬레이션 기법을 사용해서 신뢰구간을 추정.
ex) 274개의 표본에서 한 개 뽑아 기록하고 다시 넣는 것을 반복하여 통계량을 구함.
따라서, 표본의 개수는 274개이지만 무한한 것처럼 표본을 사용할 수 있음.
3) 신뢰구간에 영향을 주는 요소
: 신뢰구간이 좁을수록 예측된 모수의 범위가 좁으므로 유용함.
- 신뢰수준 낮추기 : 큰 의미는 없음
-표본의 변산성 낮추기
1. 실험과 측정을 정확히 하여 변산성을 낮춤
2. 데이터에 내재한 변산성은 없앨 수 없음
-표본의 크기를 키우기 : 가장 쉬운 방법, 그러나 시간과 비용이 증가.
4) 신뢰수준 95%에서의 오차범위 계산하기
: (1.96 * 0.5) ** 2 = 설문응답자 수
-1.96 : 신뢰수준 95%에 해당하는 값. (신뢰수준 99%일 경우, 2.58로 계산)
-0.5: 여론조사의 오차범위는 찬성 50%를 기준으로 계산
[4] 통계적 가설 검정
- 반증주의 철학에 기반하고 있어 일반적인 과학적 가설 검정과 다름
절차1) 귀무가설을 수립한다.
-귀무가설 : 기각하고자 하는 가설
-대립가설: 주장하고자 하는 가설
절차2) 유의수준을 결정한다.
-유의수준: '100% - 신뢰수준'
-신뢰수준과 반대되는 개념. 유의수준 + 신뢰수준 = 100
절차3) p-값을 계산한다.
-p-값 : 귀무가설이 참일 때 검정통계량 이상이 나올 확률
절차4) p값과 유의수준을 비교한다.
1. p > 유의수준
- 결론을 유보한다.
- 결론을 내릴 필요가 있을 경우, 데이터를 더 모은다.
- 단, 반복해서 가설검정을 할 경우 유의수준을 조정한다.
2. p < 유의수준 (이게 좋음)
- 귀무가설을 기각한다.
- 흔히 "통계적으로 유의하다"라고 표현 (현실적으로 유의미한것 x)
* p는 유의수준에 영향을 받지 않음. 따로 계산된 뒤 비교하는 것.
1) 귀무가설과 대립가설
| 귀무가설 | 대립가설 |
| -기각하고자 하는 가설 -차이가 없다, 똑같다와 같은 형태 -특별한 증거가 없으면 참으로 간주 |
-주장하고자 하는 가설 -차이가 있다, 다르다와 같은 형태 -충분한 증거가 필요 |
1. 귀무가설을 기각하는 논리
- a=>b라는 명제는 not b=>not a 라는 대우명제와 동치
- 귀무가설이 참이면(a), 현재 결과가 나올 확률이 높다(b)
- 현재 결과가 나올 확률이 낮으면(not b), 귀무가설이 거짓이다(not a)
2. 귀무가설을 채택하지 않는 논리
- 통계적 가설검정을 만든 로널드 피셔의 반증주의적 과학철학을 반영
- a=>b라는 명제가 성립해도, b=>a가 반드시 성립하는 것은 아님
- 귀무가설이 참이면(a), 현재 결과가 나올 확률이 높다(b)
- 현재 결과가 나올 확률이 높아도(b), 귀무가설이 참(a)이라고 할 수는 없음
2) 통계적 가설 검정 순서도

3) 가설 검정의 결과
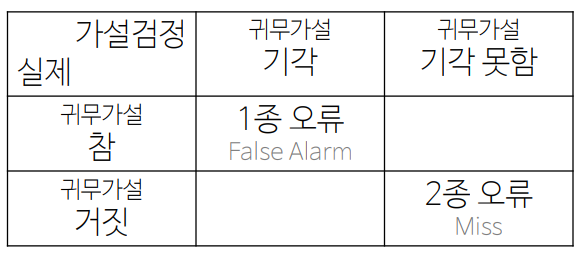
-귀무가설이 참일 경우, 1종 오류는 유의수준만큼 발생 (유의수준은 1종오류와 같다)
-유의수준을 낮추면 1종 오류가 감소하고, 2종 오류가 증가
-1종 오류와 2종 오류는 반비례하다고 보면 됨. (그 비율이 같지는 않음)
[5] A/B 테스팅
-과학분야에서 무작위 대조군 실험
-주로 웹 서비스 등의 분야에서 A/B테스팅이라는 명칭을 사용
-고객들에게 서로 다른 웹페이지나 광고를 보여주고 목표지표를 측정함.
직관만 믿고 까불었다가 망한 PM의 사연
안녕하세요, 검색 프로덕트 매니저 Demi예요.
medium.com
1) 근거기반 의학에서 근거의 수준
Level 1: 무작위 대조군 실험에서 얻어진 근거
Level 2-1: 대조군 실험에서 얻어진 근거 (무작위 할당이 아님)
Level 2-2: 동일집단 연구 등
Level 2-3: 대조군이 없는 극적인 결과 등
Level 2-4: 임상 경험에 근거한 전문가의 의견 등
2) A/B테스팅에서 중요한 점
-작은 실험을 자주, 많이 해야 한다.
-할 수 있다면 가능한 여러 가지 변수를 동시에 실험한다.
-실험을 많이 할 수 있는 기술적, 문화적 환경이 형성되어야 한다.
-당연하거나 터무니 없어보이는 아이디어도 실험할 필요가 있다.
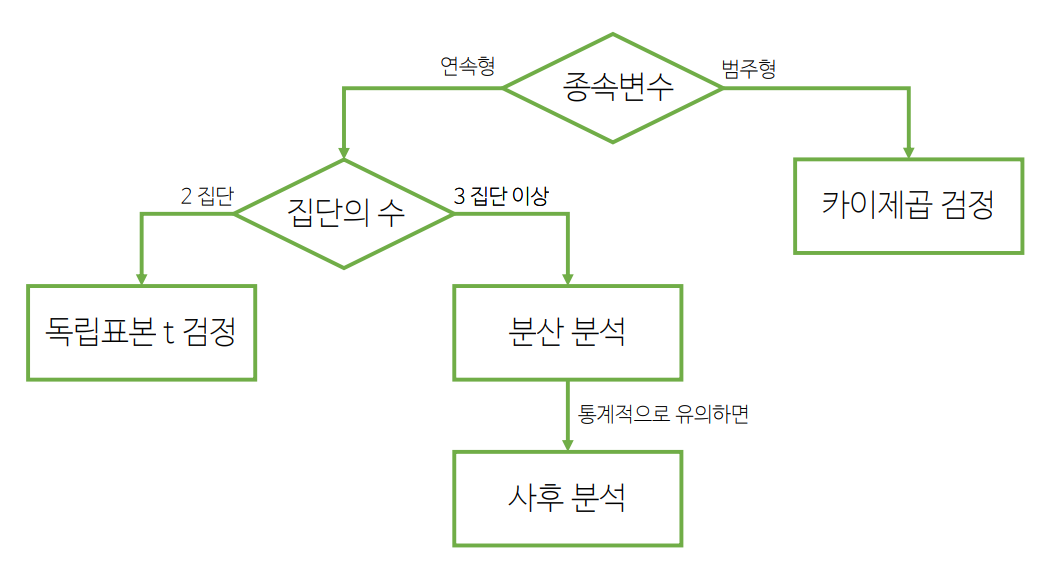
[6] 독립표본 t-검정
1) 집단 비교 통계 처리 순서도
'TIL & WIL > 통계분석' 카테고리의 다른 글
| 통계분석 4일차 (3). 회귀분석 (잔차 / 최소제곱법 / R제곱) (0) | 2023.02.16 |
|---|---|
| 통계분석 4일차 (2). 상관분석 (상관계수 / 기울기 / 공분산 / 스피어만 / 켄달) (0) | 2023.02.16 |
| 통계분석 4일차 (1). 가설검정 (1) | 2023.02.16 |
| 통계분석 3일차. 독립표본 t 검정/ 효과크기/ 대응표본 t 검정/ 분산분석 (0) | 2023.02.16 |
| 통계분석 1일차. 확률분포 / 기술통계 / 모집단과 표본 (0) | 2023.02.13 |
